Increasing amount of data is available on the web. Web scraping is a technique developed to extract data from web pages automatically and transforming it into a data format for further data analysis and insights. Applied clustering is an unsupervised learning technique that refers to a family of pattern discovery and data mining tools with applications in machine learning, bioinformatics, image analysis, and segmentation of consumer types, among others. R offers several packages and tools for web scraping, data manipulation, statistical analysis and machine learning. The motivation for this post is to illustrate the applications of web scraping, dimension reduction and applied clustering tools in R.
The original 2016 world happiness data set used for this post is no longer available at Wikipedia. Instead, code snippets in this post have been updated to scrape the 2019 World Happiness Report published at this link (https://en.wikipedia.org/wiki/World_Happiness_Report#2019_report). In this exercise, the data set was pre-processed prior to principal component analysis (PCA) and clustering. The goals of the clustering approach in this post were to segment rows of the over 156 countries in the data into separate groups (clusters), The expectation is that sets of countries within a cluster are as similar as possible to each other for happiness and social progress, and as dissimilar as possible to the other sets of countries assigned in different clusters.
Load Required Packages
require(rvest) require(magrittr) require(plyr) require(dplyr) require(reshape2) require(ggplot2) require(FactoMineR) require(factoextra) require(cluster) require(useful)
Web Scraping and Data Pre-processing
# Import data set from the site
url1 <- "https://en.wikipedia.org/wiki/World_Happiness_Report"
happy <- read_html(url1) %>%
html_nodes("table") %>%
extract2(5) %>%
html_table(fill=T)
# inspect imported data structure
str(happy)
'data.frame': 156 obs. of 9 variables:
$ Overall rank : int 1 2 3 4 5 6 7 8 9 10 ...
$ Country or region : chr "Finland" "Denmark" "Norway" "Iceland" ...
$ Score : num 7.77 7.6 7.55 7.49 7.49 ...
$ GDP per capita : num 1.34 1.38 1.49 1.38 1.4 ...
$ Social support : num 1.59 1.57 1.58 1.62 1.52 ...
$ Healthy life expectancy : num 0.986 0.996 1.028 1.026 0.999 ...
$ Freedom to make life choices: num 0.596 0.592 0.603 0.591 0.557 0.572 0.574 0.585 0.584 0.532 ...
$ Generosity : num 0.153 0.252 0.271 0.354 0.322 0.263 0.267 0.33 0.285 0.244 ...
$ Perceptions of corruption : num 0.393 0.41 0.341 0.118 0.298 0.343 0.373 0.38 0.308 0.226 ...
Pre-process the data set for analysis:
## Exclude columns with ranks and scores, retain the other columns
happy <- happy[c(2,4:9)]
### rename column headers
colnames(happy) <- gsub(" ", "_", colnames(happy), perl=TRUE)
names(happy)
[1] "Country_or_region" "GDP_per_capita" "Social_support"
[4] "Healthy_life_expectancy" "Freedom_to_make_life_choices" "Generosity"
[7] "Perceptions_of_corruption"
Check for missing values in the data set
mean(is.na(happy[, 2:7])) ## [1] 0
There are no missing values. The code below will generate summary statistics of the raw data.
summary(happy[,2:7]) GDP per capita Social support Healthy life expectancy Freedom to make life choices Generosity Min. :0.0000 Min. :0.000 Min. :0.0000 Min. :0.000 Min. :0.0000 1st Qu.:0.6028 1st Qu.:1.056 1st Qu.:0.5477 1st Qu.:0.308 1st Qu.:0.1087 Median :0.9600 Median :1.272 Median :0.7890 Median :0.417 Median :0.1795 Mean :0.9023 Mean :1.209 Mean :0.7254 Mean :0.393 Mean :0.1862 3rd Qu.:1.2235 3rd Qu.:1.452 3rd Qu.:0.8818 3rd Qu.:0.508 3rd Qu.:0.2520 Max. :1.6840 Max. :1.624 Max. :1.1410 Max. :0.631 Max. :0.5660 Perceptions of corruption Min. :0.0000 1st Qu.:0.0465 Median :0.0850 Mean :0.1102 3rd Qu.:0.1412 Max. :0.4530
An important procedure for meaningful clustering and dimension reduction steps involves data transformation and scaling variables. The simple function below will transform all variables to values between 0 and 1.
## transform variables to a range of 0 to 1
range_transform <- function(x) {
(x - min(x))/(max(x)-min(x))
}
happy[,2:7] <- as.data.frame(apply(happy[,2:7], 2, range_transform))
### summary of transformed data shows success of transformation
summary(happy[,2:7])
GDP per capita Social support Healthy life expectancy Freedom to make life choices Generosity
Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
1st Qu.:0.3579 1st Qu.:0.6501 1st Qu.:0.4801 1st Qu.:0.4881 1st Qu.:0.1921
Median :0.5701 Median :0.7829 Median :0.6915 Median :0.6609 Median :0.3171
Mean :0.5358 Mean :0.7447 Mean :0.6357 Mean :0.6228 Mean :0.3290
3rd Qu.:0.7265 3rd Qu.:0.8944 3rd Qu.:0.7728 3rd Qu.:0.8051 3rd Qu.:0.4452
Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
Perceptions of corruption
Min. :0.0000
1st Qu.:0.1026
Median :0.1876
Mean :0.2432
3rd Qu.:0.3118
Max. :1.0000
Although the previous data transformation step could have been adequate for next steps of this analysis, the function shown below as an example of data transformation will re-scale all variables to a mean of 0 and standard deviation of 1.
## Scaling variables to a mean of 0 and standard deviation of 1.
sd_scale <- function(x) {
(x - mean(x))/sd(x)
}
happy[,2:7] <- as.data.frame(apply(happy[,2:7], 2, sd_scale))
### summary of the scaled data
summary(happy[,2:7])
GDP per capita Social support Healthy life expectancy Freedom to make life choices Generosity
Min. :-2.2803 Min. :-4.0381 Min. :-2.9953 Min. :-2.7353 Min. :-1.93585
1st Qu.:-0.7570 1st Qu.:-0.5130 1st Qu.:-0.7334 1st Qu.:-0.5915 1st Qu.:-0.80544
Median : 0.1459 Median : 0.2074 Median : 0.2627 Median : 0.1672 Median :-0.07003
Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.00000
3rd Qu.: 0.8119 3rd Qu.: 0.8117 3rd Qu.: 0.6457 3rd Qu.: 0.8006 3rd Qu.: 0.68357
Max. : 1.9757 Max. : 1.3844 Max. : 1.7162 Max. : 1.6567 Max. : 3.94746
Perceptions of corruption
Min. :-1.1625
1st Qu.:-0.6718
Median :-0.2655
Mean : 0.0000
3rd Qu.: 0.3281
Max. : 3.6179
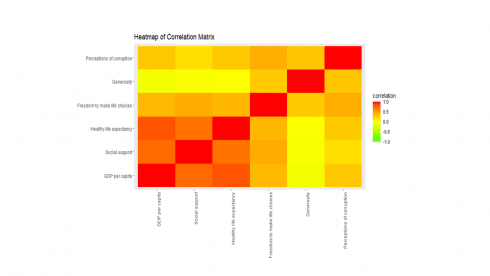
Simple Correlation Analysis
Now, the data is ready to explore variable relationships with each other.
corr <- cor(happy[, 2:7], method="pearson")
ggplot(melt(corr, varnames=c("x", "y"), value.name="correlation"),
aes(x=x, y=y)) +
geom_tile(aes(fill=correlation)) +
scale_fill_gradient2(low="green", mid="yellow", high="red",
guide=guide_colorbar(ticks=FALSE, barheight = 5),
limits=c(-1,1)) +
theme(axis.text.x = element_text(angle = 90, hjust = 1)) +
labs(title="Heatmap of Correlation Matrix",
x=NULL, y=NULL)
Principal Component Analysis
Principal component analysis is a multivariate statistics widely used for examining relationships among several quantitative variables. PCA identifies patterns in the variables to reduce the dimensions of the data set in multiple regression and clustering, among others.
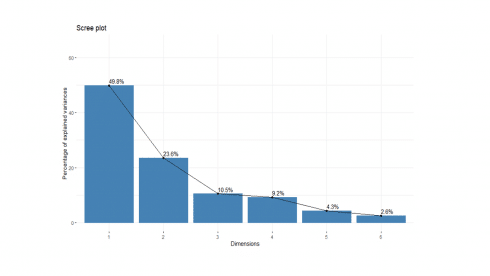
soc.pca <- PCA(happy[, 2:7], graph=FALSE) fviz_screeplot(soc.pca, addlabels = TRUE, ylim = c(0, 65))
The percentages on each bar indicate the proportion of total variance explained by the respective principal component. As seen in the scree plot, the first three principal components accounted for ~84% of the total variance.
soc.pca$eig eigenvalue percentage of variance cumulative percentage of variance comp 1 2.9904701 49.841169 49.84117 comp 2 1.4130577 23.550961 73.39213 comp 3 0.6307329 10.512215 83.90435 comp 4 0.5518763 9.197939 93.10228 comp 5 0.2605080 4.341800 97.44408 comp 6 0.1533550 2.555916 100.00000
The output suggests that the first two principal components are worthy of consideration. A practical guide to determining the optimum number of principal component axes could be to consider only those components with eigen values greater than or equal to 1.
# Contributions of variables to principal components
soc.pca$var$contrib[,1:3]
Dim.1 Dim.2 Dim.3
GDP per capita 26.5456729 5.280318 0.11986429
Social support 24.1053873 4.864469 7.67197216
Healthy life expectancy 26.1002417 3.822251 0.02279907
Freedom to make life choices 14.4674975 12.952726 2.52299300
Generosity 0.4263867 48.134912 30.49214676
Perceptions of corruption 8.3548139 24.945324 59.17022472
The first principal component explained approximately 50% of the total variation and appears to represent opportunity, GDP per capita, healthy life expectancy, and social support.
The second principal component explained a further 24% of the total variation and represented generosity, perception of corruption.
Applied Clustering
The syntax for clustering algorithms require specifying the number of desired clusters (k=) as an input. The practical issue is what value should k take? In the absence of a subject-matter knowledge, R offers various empirical approaches for selecting a value of k. One such R tool for suggested best number of clusters is the NbClust package.
require(NbClust)
nbc <- NbClust(happy[, 2:7], distance="manhattan",
min.nc=2, max.nc=30, method="ward.D", index='all')
*** : The Hubert index is a graphical method of determining the number of clusters.
In the plot of Hubert index, we seek a significant knee that corresponds to a
significant increase of the value of the measure i.e the significant peak in Hubert
index second differences plot.
*** : The D index is a graphical method of determining the number of clusters.
In the plot of D index, we seek a significant knee (the significant peak in Dindex
second differences plot) that corresponds to a significant increase of the value of
the measure.
*******************************************************************
* Among all indices:
* 3 proposed 2 as the best number of clusters
* 11 proposed 3 as the best number of clusters
* 3 proposed 4 as the best number of clusters
* 1 proposed 8 as the best number of clusters
* 1 proposed 11 as the best number of clusters
* 1 proposed 23 as the best number of clusters
* 1 proposed 27 as the best number of clusters
* 2 proposed 30 as the best number of clusters
***** Conclusion *****
* According to the majority rule, the best number of clusters is 3
The NbClust algorithm suggested a 3-cluster solution to the combined data set. So, we will apply K=3 in next steps.
set.seed(4653) pamK3 <- pam(happy[, 2:7], diss=FALSE, 3, keep.data=TRUE) # Number of countries assigned in the three clusters fviz_silhouette(pamK3) cluster size ave.sil.width 1 1 29 0.34 2 2 78 0.37 3 3 49 0.27
The number of countries assigned in each cluster is displayed in the table above. The second cluster contains half of the total number of countries.
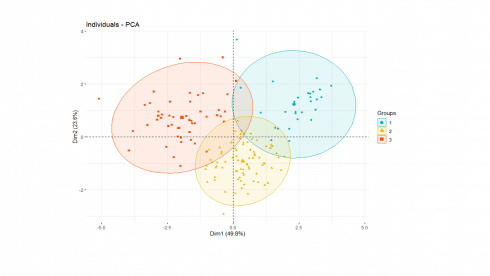
Putting it together
We can now display individual countries and superimpose their cluster assignments on the plane defined by the first two principal components.
happy['cluster'] <- as.factor(pamK3$clustering)
fviz_pca_ind(soc.pca,
label="none",
habillage = happy$cluster, #color by cluster
palette = c("#00AFBB", "#E7B800", "#FC4E07", "#7CAE00", "#C77CFF", "#00BFC4"),
addEllipses=TRUE
)
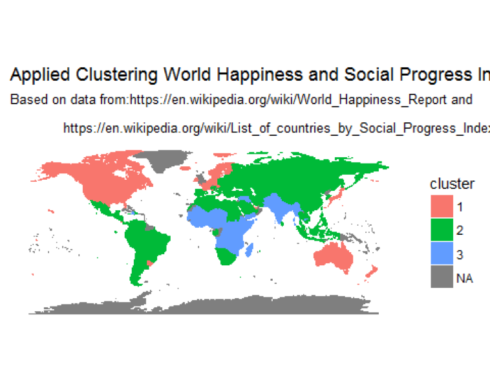
Finally, displaying clusters of countries on a world map
Standardize country names to confirm with country names in the map dataset
happy$Country <- as.character(mapvalues(happy$Country_or_region,
from = c("United States of America", 'Congo (Kinshasa)', 'Trinidad & Tobago'),
to=c("USA", "Democratic Republic of the Congo", 'Trinidad')))
load world map data in memory and left join with the world happiness data set.
map.world <- map_data("world")
# LEFT JOIN
map.world_joined <- left_join(map.world, happy, by = c('region' = 'Country'))
ggplot() +
geom_polygon(data = map.world_joined, aes(x = long, y = lat, group = group, fill=cluster, color=cluster)) +
labs(title = "Applied Clustering World Happiness and Social Progress Index",
subtitle = "Based on data from:https://en.wikipedia.org/wiki/World_Happiness_Report and\n
https://en.wikipedia.org/wiki/List_of_countries_by_Social_Progress_Index",
x=NULL, y=NULL) +
coord_equal() +
theme(panel.grid.major=element_blank(),
panel.grid.minor=element_blank(),
axis.text.x=element_blank(),
axis.text.y=element_blank(),
axis.ticks=element_blank(),
panel.background=element_blank()
)
Concluding Remarks
Cluster analysis and dimension reduction algorithms such as PCA are widely used approaches to split data sets into distinct subsets of groups as well as to reduce the dimensionality of the variables, respectively. Together, these analytics approaches: 1) make the structure of the data easier to understand, and 2) also make subsequent data mining tasks easier to perform. Hopefully, this post has attempted to illustrate the applications of web scraping, pre-processing data for analysis, PCA, and cluster analysis using various tools available in R. Please let us know your comments and suggestions.