Hello everyone, hope you had a wonderful Christmas! In this post I will show you how to do k means clustering in R. We will use the iris dataset from the datasets library.
What is K Means Clustering?
K Means Clustering is an unsupervised learning algorithm that tries to cluster data based on their similarity. Unsupervised learning means that there is no outcome to be predicted, and the algorithm just tries to find patterns in the data. In k means clustering, we have to specify the number of clusters we want the data to be grouped into. The algorithm randomly assigns each observation to a cluster, and finds the centroid of each cluster. Then, the algorithm iterates through two steps:
- Reassign data points to the cluster whose centroid is closest.
- Calculate new centroid of each cluster.
These two steps are repeated till the within cluster variation cannot be reduced any further. The within cluster variation is calculated as the sum of the euclidean distance between the data points and their respective cluster centroids.
Exploring the data
The iris dataset contains data about sepal length, sepal width, petal length, and petal width of flowers of different species. Let us see what it looks like:
library(datasets) head(iris) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3.0 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5.0 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa
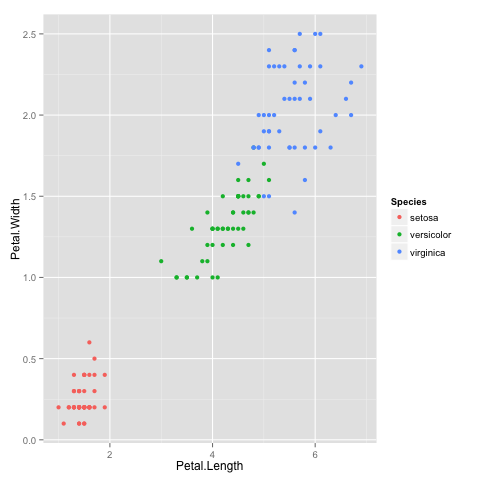
After a little bit of exploration, I found that Petal.Length and Petal.Width were similar among the same species but varied considerably between different species, as demonstrated below:
library(ggplot2) ggplot(iris, aes(Petal.Length, Petal.Width, color = Species)) + geom_point()
Clustering
Okay, now that we have seen the data, let us try to cluster it. Since the initial cluster assignments are random, let us set the seed to ensure reproducibility.
set.seed(20) irisCluster <- kmeans(iris[, 3:4], 3, nstart = 20) irisCluster K-means clustering with 3 clusters of sizes 46, 54, 50 Cluster means: Petal.Length Petal.Width 1 5.626087 2.047826 2 4.292593 1.359259 3 1.462000 0.246000 Clustering vector: [1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 [35] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 [69] 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 [103] 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 2 1 1 2 2 1 1 1 1 1 1 1 1 [137] 1 1 2 1 1 1 1 1 1 1 1 1 1 1 Within cluster sum of squares by cluster: [1] 15.16348 14.22741 2.02200 (between_SS / total_SS = 94.3 %) Available components: [1] "cluster" "centers" "totss" "withinss" [5] "tot.withinss" "betweenss" "size" "iter" [9] "ifault"
Since we know that there are 3 species involved, we ask the algorithm to group the data into 3 clusters, and since the starting assignments are random, we specify nstart = 20. This means that R will try 20 different random starting assignments and then select the one with the lowest within cluster variation.
We can see the cluster centroids, the clusters that each data point was assigned to, and the within cluster variation.
Let us compare the clusters with the species.
table(irisCluster$cluster, iris$Species)
setosa versicolor virginica
1 0 2 44
2 0 48 6
3 50 0 0
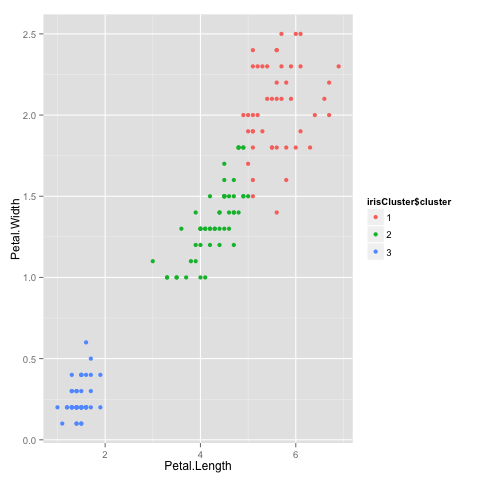
As we can see, the data belonging to the setosa species got grouped into cluster 3, versicolor into cluster 2, and virginica into cluster 1. The algorithm wrongly classified two data points belonging to versicolor and six data points belonging to virginica.
We can also plot the data to see the clusters:
irisCluster$cluster <- as.factor(irisCluster$cluster) ggplot(iris, aes(Petal.Length, Petal.Width, color = irisCluster$cluster)) + geom_point()
That brings us to the end of the article. I hope you enjoyed it! If you have any questions or feedback, feel free to leave a comment or reach out to me on Twitter.