This is the second part of the 4-series articles about Dow Jones Stock Market. To read the first part go to this link. In this part, I am going to analyze the Dow Jones Industrial Average (DJIA) trade volume.
Packages
The packages being used in this post series are herein listed.
suppressPackageStartupMessages(library(lubridate))
suppressPackageStartupMessages(library(fBasics))
suppressPackageStartupMessages(library(lmtest))
suppressPackageStartupMessages(library(urca))
suppressPackageStartupMessages(library(ggplot2))
suppressPackageStartupMessages(library(quantmod))
suppressPackageStartupMessages(library(PerformanceAnalytics))
suppressPackageStartupMessages(library(rugarch))
suppressPackageStartupMessages(library(FinTS))
suppressPackageStartupMessages(library(forecast))
suppressPackageStartupMessages(library(strucchange))
suppressPackageStartupMessages(library(TSA))
Getting Data
We upload the environment status as saved at the end of part 1.
load(file='DowEnvironment.RData')
Daily Volume Exploratory Analysis
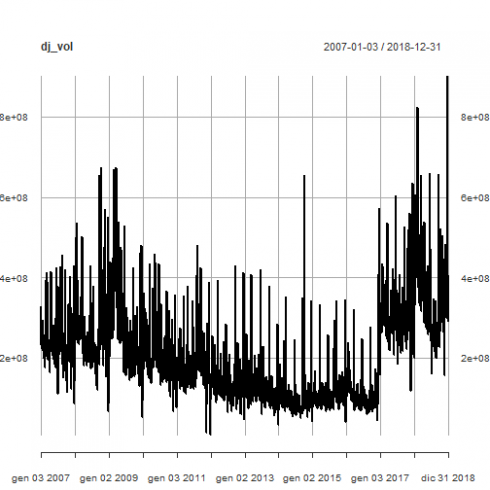
From the saved environment, we can find back our DJI object. We plot the daily volume.
dj_vol <- DJI[,"DJI.Volume"]
plot(dj_vol)
It is remarkable the level jump at the beginning of 2017, something that we will investigate in part 4.
We transform the volume time series data and timeline index into a dataframe.
dj_vol_df <- xts_to_dataframe(dj_vol)
head(dj_vol_df)
## year value
## 1 2007 327200000
## 2 2007 259060000
## 3 2007 235220000
## 4 2007 223500000
## 5 2007 225190000
## 6 2007 226570000
tail(dj_vol_df)
## year value
## 3015 2018 900510000
## 3016 2018 308420000
## 3017 2018 433080000
## 3018 2018 407940000
## 3019 2018 336510000
## 3020 2018 288830000
Basic statistics summary
(dj_stats <- dataframe_basicstats(dj_vol_df))
## 2007 2008 2009 2010
## nobs 2.510000e+02 2.530000e+02 2.520000e+02 2.520000e+02
## NAs 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## Minimum 8.640000e+07 6.693000e+07 5.267000e+07 6.840000e+07
## Maximum 4.571500e+08 6.749200e+08 6.729500e+08 4.598900e+08
## 1. Quartile 2.063000e+08 2.132100e+08 1.961850e+08 1.633400e+08
## 3. Quartile 2.727400e+08 3.210100e+08 3.353625e+08 2.219025e+08
## Mean 2.449575e+08 2.767164e+08 2.800537e+08 2.017934e+08
## Median 2.350900e+08 2.569700e+08 2.443200e+08 1.905050e+08
## Sum 6.148432e+10 7.000924e+10 7.057354e+10 5.085193e+10
## SE Mean 3.842261e+06 5.965786e+06 7.289666e+06 3.950031e+06
## LCL Mean 2.373901e+08 2.649672e+08 2.656970e+08 1.940139e+08
## UCL Mean 2.525248e+08 2.884655e+08 2.944104e+08 2.095728e+08
## Variance 3.705505e+15 9.004422e+15 1.339109e+16 3.931891e+15
## Stdev 6.087286e+07 9.489163e+07 1.157199e+08 6.270480e+07
## Skewness 9.422400e-01 1.203283e+00 1.037015e+00 1.452082e+00
## Kurtosis 1.482540e+00 2.064821e+00 6.584810e-01 3.214065e+00
## 2011 2012 2013 2014
## nobs 2.520000e+02 2.500000e+02 2.520000e+02 2.520000e+02
## NAs 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## Minimum 8.410000e+06 4.771000e+07 3.364000e+07 4.287000e+07
## Maximum 4.799800e+08 4.296100e+08 4.200800e+08 6.554500e+08
## 1. Quartile 1.458775e+08 1.107150e+08 9.488000e+07 7.283000e+07
## 3. Quartile 1.932400e+08 1.421775e+08 1.297575e+08 9.928000e+07
## Mean 1.804133e+08 1.312606e+08 1.184434e+08 9.288516e+07
## Median 1.671250e+08 1.251950e+08 1.109250e+08 8.144500e+07
## Sum 4.546415e+10 3.281515e+10 2.984773e+10 2.340706e+10
## SE Mean 3.897738e+06 2.796503e+06 2.809128e+06 3.282643e+06
## LCL Mean 1.727369e+08 1.257528e+08 1.129109e+08 8.642012e+07
## UCL Mean 1.880897e+08 1.367684e+08 1.239758e+08 9.935019e+07
## Variance 3.828475e+15 1.955108e+15 1.988583e+15 2.715488e+15
## Stdev 6.187468e+07 4.421660e+07 4.459353e+07 5.211034e+07
## Skewness 1.878239e+00 3.454971e+00 3.551752e+00 6.619268e+00
## Kurtosis 5.631080e+00 1.852581e+01 1.900989e+01 5.856136e+01
## 2015 2016 2017 2018
## nobs 2.520000e+02 2.520000e+02 2.510000e+02 2.510000e+02
## NAs 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## Minimum 4.035000e+07 4.589000e+07 1.186100e+08 1.559400e+08
## Maximum 3.445600e+08 5.734700e+08 6.357400e+08 9.005100e+08
## 1. Quartile 8.775250e+07 8.224250e+07 2.695850e+08 2.819550e+08
## 3. Quartile 1.192150e+08 1.203550e+08 3.389950e+08 4.179200e+08
## Mean 1.093957e+08 1.172089e+08 3.112396e+08 3.593710e+08
## Median 1.021000e+08 9.410500e+07 2.996700e+08 3.414700e+08
## Sum 2.756772e+10 2.953664e+10 7.812114e+10 9.020213e+10
## SE Mean 2.433611e+06 4.331290e+06 4.376432e+06 6.984484e+06
## LCL Mean 1.046028e+08 1.086786e+08 3.026202e+08 3.456151e+08
## UCL Mean 1.141886e+08 1.257392e+08 3.198590e+08 3.731270e+08
## Variance 1.492461e+15 4.727538e+15 4.807442e+15 1.224454e+16
## Stdev 3.863238e+07 6.875709e+07 6.933572e+07 1.106550e+08
## Skewness 3.420032e+00 3.046742e+00 1.478708e+00 1.363823e+00
## Kurtosis 1.612326e+01 1.122161e+01 3.848619e+00 3.277164e+00
In the following, we make specific comments to some relevant above shown metrics.
Mean
Years when Dow Jones daily volume has positive mean are:
filter_dj_stats(dj_stats, "Mean", 0)
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"
All Dow Jones daily volume mean values in ascending order.
dj_stats["Mean",order(dj_stats["Mean",,])]
## 2014 2015 2016 2013 2012 2011 2010
## Mean 92885159 109395714 117208889 118443373 131260600 180413294 201793373
## 2007 2008 2009 2017 2018
## Mean 244957450 276716364 280053730 311239602 359371036
Median
Years when Dow Jones daily volume has positive median are:
filter_dj_stats(dj_stats, "Median", 0)
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"
All Dow Jones daily volume median values in ascending order.
dj_stats["Median",order(dj_stats["Median",,])]
## 2014 2016 2015 2013 2012 2011 2010
## Median 81445000 94105000 102100000 110925000 125195000 167125000 190505000
## 2007 2009 2008 2017 2018
## Median 235090000 244320000 256970000 299670000 341470000
Skewness
Years when Dow Jones daily volume has positive skewness are:
filter_dj_stats(dj_stats, "Skewness", 0)
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"
All Dow Jones daily volume skewness values in ascending order.
dj_stats["Skewness",order(dj_stats["Skewness",,])]
## 2007 2009 2008 2018 2010 2017 2011
## Skewness 0.94224 1.037015 1.203283 1.363823 1.452082 1.478708 1.878239
## 2016 2015 2012 2013 2014
## Skewness 3.046742 3.420032 3.454971 3.551752 6.619268
Excess Kurtosis
Years when Dow Jones daily volume has positive excess kurtosis are:
filter_dj_stats(dj_stats, "Kurtosis", 0)
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"
All Dow Jones daily volume excess kurtosis values in ascending order.
dj_stats["Kurtosis",order(dj_stats["Kurtosis",,])]
## 2009 2007 2008 2010 2018 2017 2011
## Kurtosis 0.658481 1.48254 2.064821 3.214065 3.277164 3.848619 5.63108
## 2016 2015 2012 2013 2014
## Kurtosis 11.22161 16.12326 18.52581 19.00989 58.56136
Box-plots
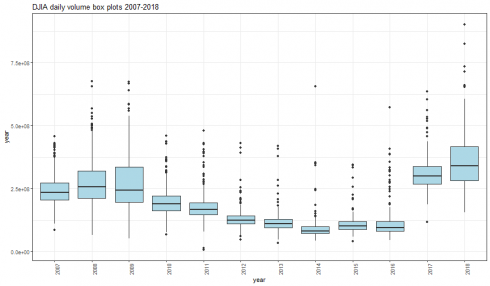
dataframe_boxplot(dj_vol_df, "DJIA daily volume box plots 2007-2018")
The trade volume starts to decrease from 2010 and on 2017 a remarkable increase occurred. Year 2018 volume has been even larger than 2017 and other years as well.
Density plots
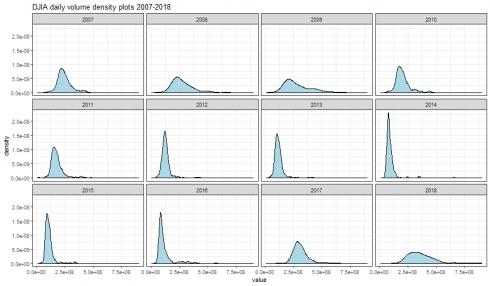
dataframe_densityplot(dj_vol_df, "DJIA daily volume density plots 2007-2018")
Shapiro Tests
dataframe_shapirotest(dj_vol_df)
## result
## 2007 6.608332e-09
## 2008 3.555102e-10
## 2009 1.023147e-10
## 2010 9.890576e-13
## 2011 2.681476e-16
## 2012 1.866544e-20
## 2013 6.906596e-21
## 2014 5.304227e-27
## 2015 2.739912e-21
## 2016 6.640215e-23
## 2017 4.543843e-12
## 2018 9.288371e-11
The null hypothesis of normality is rejected for all years.
QQ plots
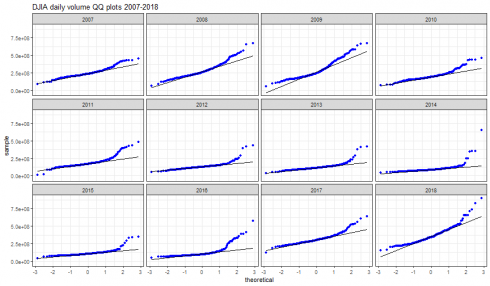
dataframe_qqplot(dj_vol_df, "DJIA daily volume QQ plots 2007-2018")
QQplots visually confirm the non-normality of daily trade volume distribution.
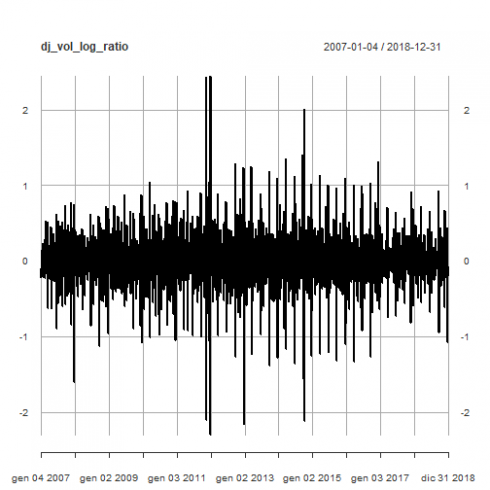
Daily volume log-ratio Exploratory Analysis
Similarly to log-returns, we can define the trade volume log ratio as.
\[
v_{t}\ := ln \frac{V_{t}}{V_{t-1}}
\]
We can compute it by CalculateReturns within the PerformanceAnalytics package and plot it.
dj_vol_log_ratio <- CalculateReturns(dj_vol, "log")
dj_vol_log_ratio <- na.omit(dj_vol_log_ratio)
plot(dj_vol_log_ratio)
Mapping the trade volume log-ratio time series data and timeline index into a dataframe.
dj_vol_df <- xts_to_dataframe(dj_vol_log_ratio)
head(dj_vol_df)
## year value
## 1 2007 -0.233511910
## 2 2007 -0.096538449
## 3 2007 -0.051109832
## 4 2007 0.007533076
## 5 2007 0.006109458
## 6 2007 0.144221282
tail(dj_vol_df)
## year value
## 3014 2018 0.44563907
## 3015 2018 -1.07149878
## 3016 2018 0.33945998
## 3017 2018 -0.05980236
## 3018 2018 -0.19249224
## 3019 2018 -0.15278959
Basic statistics summary
(dj_stats <- dataframe_basicstats(dj_vol_df))
## 2007 2008 2009 2010 2011
## nobs 250.000000 253.000000 252.000000 252.000000 252.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -1.606192 -1.122526 -1.071225 -1.050181 -2.301514
## Maximum 0.775961 0.724762 0.881352 1.041216 2.441882
## 1. Quartile -0.123124 -0.128815 -0.162191 -0.170486 -0.157758
## 3. Quartile 0.130056 0.145512 0.169233 0.179903 0.137108
## Mean -0.002685 0.001203 -0.001973 -0.001550 0.000140
## Median -0.010972 0.002222 -0.031748 -0.004217 -0.012839
## Sum -0.671142 0.304462 -0.497073 -0.390677 0.035162
## SE Mean 0.016984 0.016196 0.017618 0.019318 0.026038
## LCL Mean -0.036135 -0.030693 -0.036670 -0.039596 -0.051141
## UCL Mean 0.030766 0.033100 0.032725 0.036495 0.051420
## Variance 0.072112 0.066364 0.078219 0.094041 0.170850
## Stdev 0.268536 0.257612 0.279677 0.306661 0.413341
## Skewness -0.802037 -0.632586 0.066535 -0.150523 0.407226
## Kurtosis 5.345212 2.616615 1.500979 1.353797 14.554642
## 2012 2013 2014 2015 2016
## nobs 250.000000 252.000000 252.000000 252.000000 252.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -2.158960 -1.386215 -2.110572 -1.326016 -1.336471
## Maximum 1.292956 1.245202 2.008667 1.130289 1.319713
## 1. Quartile -0.152899 -0.145444 -0.144280 -0.143969 -0.134011
## 3. Quartile 0.144257 0.149787 0.134198 0.150003 0.141287
## Mean 0.001642 -0.002442 0.000200 0.000488 0.004228
## Median -0.000010 -0.004922 0.013460 0.004112 -0.002044
## Sum 0.410521 -0.615419 0.050506 0.123080 1.065480
## SE Mean 0.021293 0.019799 0.023514 0.019010 0.019089
## LCL Mean -0.040295 -0.041435 -0.046110 -0.036952 -0.033367
## UCL Mean 0.043579 0.036551 0.046510 0.037929 0.041823
## Variance 0.113345 0.098784 0.139334 0.091071 0.091826
## Stdev 0.336667 0.314299 0.373274 0.301780 0.303028
## Skewness -0.878227 -0.297951 -0.209417 -0.285918 0.083826
## Kurtosis 8.115847 4.681120 9.850061 4.754926 4.647785
## 2017 2018
## nobs 251.000000 251.000000
## NAs 0.000000 0.000000
## Minimum -0.817978 -1.071499
## Maximum 0.915599 0.926101
## 1. Quartile -0.112190 -0.119086
## 3. Quartile 0.110989 0.112424
## Mean -0.000017 0.000257
## Median -0.006322 0.003987
## Sum -0.004238 0.064605
## SE Mean 0.013446 0.014180
## LCL Mean -0.026500 -0.027671
## UCL Mean 0.026466 0.028185
## Variance 0.045383 0.050471
## Stdev 0.213032 0.224658
## Skewness 0.088511 -0.281007
## Kurtosis 3.411036 4.335748
In the following, we make specific comments to some relevant above-shown metrics.
Mean
Years when Dow Jones daily volume log-ratio has positive mean are:
filter_dj_stats(dj_stats, "Mean", 0)
## [1] "2008" "2011" "2012" "2014" "2015" "2016" "2018"
All Dow Jones daily volume log-ratio mean values in ascending order.
dj_stats["Mean",order(dj_stats["Mean",,])]
## 2007 2013 2009 2010 2017 2011 2014
## Mean -0.002685 -0.002442 -0.001973 -0.00155 -1.7e-05 0.00014 2e-04
## 2018 2015 2008 2012 2016
## Mean 0.000257 0.000488 0.001203 0.001642 0.004228
Median
Years when Dow Jones daily volume log-ratio has positive median are:
filter_dj_stats(dj_stats, "Median", 0)
## [1] "2008" "2014" "2015" "2018"
All Dow Jones daily volume log-ratio median values in ascending order.
dj_stats["Median",order(dj_stats["Median",,])]
## 2009 2011 2007 2017 2013 2010
## Median -0.031748 -0.012839 -0.010972 -0.006322 -0.004922 -0.004217
## 2016 2012 2008 2018 2015 2014
## Median -0.002044 -1e-05 0.002222 0.003987 0.004112 0.01346
Skewness
Years when Dow Jones daily volume log-ratio has positive skewness are:
filter_dj_stats(dj_stats, "Skewness", 0)
## [1] "2009" "2011" "2016" "2017"
All Dow Jones daily volume log-ratio mean values in ascending order.
dj_stats["Skewness",order(dj_stats["Skewness",,])]
## 2012 2007 2008 2013 2015 2018
## Skewness -0.878227 -0.802037 -0.632586 -0.297951 -0.285918 -0.281007
## 2014 2010 2009 2016 2017 2011
## Skewness -0.209417 -0.150523 0.066535 0.083826 0.088511 0.407226
Excess Kurtosis
Years when Dow Jones daily volume has positive excess kurtosis are:
filter_dj_stats(dj_stats, "Kurtosis", 0)
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"
All Dow Jones daily volume log-ratio excess kurtosis values in ascending order.
dj_stats["Kurtosis",order(dj_stats["Kurtosis",,])]
## 2010 2009 2008 2017 2018 2016 2013
## Kurtosis 1.353797 1.500979 2.616615 3.411036 4.335748 4.647785 4.68112
## 2015 2007 2012 2014 2011
## Kurtosis 4.754926 5.345212 8.115847 9.850061 14.55464
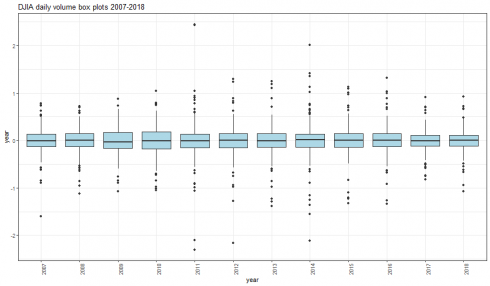
Box-plots
dataframe_boxplot(dj_vol_df, "DJIA daily volume box plots 2007-2018")
The most positive extreme values can be spotted on years 2011, 2014 and 2016. The most negative extreme values, on years 2007, 2011, 2012, 2014.
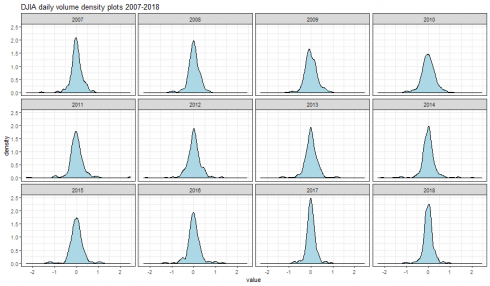
Density plots
dataframe_densityplot(dj_vol_df, "DJIA daily volume density plots 2007-2018")
Shapiro Tests
dataframe_shapirotest(dj_vol_df)
## result
## 2007 3.695053e-09
## 2008 6.160136e-07
## 2009 2.083475e-04
## 2010 1.500060e-03
## 2011 3.434415e-18
## 2012 8.417627e-12
## 2013 1.165184e-10
## 2014 1.954662e-16
## 2015 5.261037e-11
## 2016 7.144940e-11
## 2017 1.551041e-08
## 2018 3.069196e-09
Based on reported p-values, for all we can reject the null hypothesis of normal distribution.
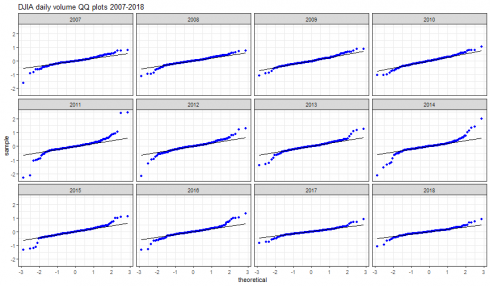
QQ plots
dataframe_qqplot(dj_vol_df, "DJIA daily volume QQ plots 2007-2018")
Departure from normality can be spotted for all reported years.
Saving the current enviroment for further analysis.
save.image(file='DowEnvironment.RData')
If you have any questions, please feel free to comment below.
References
- Dow Jones Industrial Average
- Skewness
- Kurtosis
- An introduction to analysis of financial data with R, Wiley, Ruey S. Tsay
- Time series analysis and its applications, Springer ed., R.H. Shumway, D.S. Stoffer
- Applied Econometric Time Series, Wiley, W. Enders, 4th ed.
- Forecasting – Principle and Practice, Texts, R.J. Hyndman
- Options, Futures and other Derivatives, Pearson ed., J.C. Hull
- An introduction to rugarch package
- Applied Econometrics with R, Achim Zeileis, Christian Kleiber – Springer Ed.
- GARCH modeling: diagnostic tests
Disclaimer
Any securities or databases referred in this post are solely for illustration purposes, and under no regard should the findings presented here be interpreted as investment advice or promotion of any particular security or source.