Market Basket Analysis is one of the key techniques used by large retailers to uncover associations between items. It works by looking for combinations of items that occur together frequently in transactions. To put it another way, it allows retailers to identify relationships between the items that people buy.
Association Rules are widely used to analyze retail basket or transaction data, and are intended to identify strong rules discovered in transaction data using measures of interestingness, based on the concept of strong rules.
An example of Association Rules
-
* Assume there are 100 customers
* 10 of them bought milk, 8 bought butter and 6 bought both of them
* bought milk => bought butter
* support = P(Milk & Butter) = 6/100 = 0.06
* confidence = support/P(Butter) = 0.06/0.08 = 0.75
* lift = confidence/P(Milk) = 0.75/0.10 = 7.5
Note: this example is extremely small. In practice, a rule needs the support of several hundred transactions, before it can be considered statistically significant, and datasets often contain thousands or millions of transactions.
Ok, enough for the theory, let’s get to the code.
The dataset we are using today comes from UCI Machine Learning repository. The dataset is called “Online Retail” and can be found here. It contains all the transactions occurring between 01/12/2010 and 09/12/2011 for a UK-based and registered online retailer.
Load the packages
library(tidyverse) library(readxl) library(knitr) library(ggplot2) library(lubridate) library(arules) library(arulesViz) library(plyr)
Data preprocessing and exploring
retail <- read_excel('Online_retail.xlsx')
retail <- retail[complete.cases(retail), ]
retail %>% mutate(Description = as.factor(Description))
retail %>% mutate(Country = as.factor(Country))
retail$Date <- as.Date(retail$InvoiceDate)
retail$Time <- format(retail$InvoiceDate,"%H:%M:%S")
retail$InvoiceNo <- as.numeric(as.character(retail$InvoiceNo))
glimpse(retail)
Observations: 406,829
Variables: 10
$ InvoiceNo 536365, 536365, 536365, 536365, 536365, 536365, 536365, 53...
$ StockCode "85123A", "71053", "84406B", "84029G", "84029E", "22752", ...
$ Description WHITE HANGING HEART T-LIGHT HOLDER, WHITE METAL LANTERN, ...
$ Quantity 6, 6, 8, 6, 6, 2, 6, 6, 6, 32, 6, 6, 8, 6, 6, 3, 2, 3, 3, ...
$ InvoiceDate 2010-12-01 08:26:00, 2010-12-01 08:26:00, 2010-12-01 08:2...
$ UnitPrice 2.55, 3.39, 2.75, 3.39, 3.39, 7.65, 4.25, 1.85, 1.85, 1.69...
$ CustomerID 17850, 17850, 17850, 17850, 17850, 17850, 17850, 17850, 17...
$ Country United Kingdom, United Kingdom, United Kingdom, United Ki...
$ Date 2010-12-01, 2010-12-01, 2010-12-01, 2010-12-01, 2010-12-0...
$ Time "08:26:00", "08:26:00", "08:26:00", "08:26:00", "08:26:00"...
After preprocessing, the dataset includes 406,829 records and 10 fields: InvoiceNo, StockCode, Description, Quantity, InvoiceDate, UnitPrice, CustomerID, Country, Date, Time.
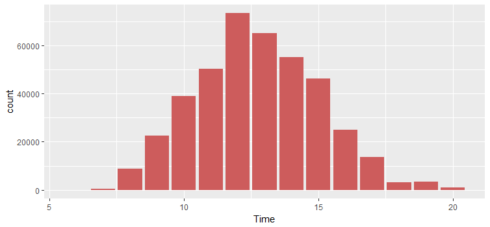
What time do people often purchase online?
In order to find the answer to this question, we need to extract “hour” from the time column.
retail$Time <- as.factor(retail$Time) a %>% ggplot(aes(x=Time)) + geom_histogram(stat="count",fill="indianred")
There is a clear bias between the hour of day and order volume. Most orders happened between 10:00–15:00.
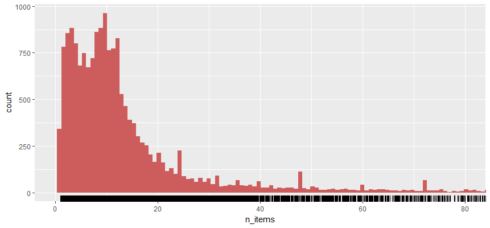
How many items each customer buy?
detach("package:plyr", unload=TRUE)
retail %>%
group_by(InvoiceNo) %>%
summarize(n_items = mean(Quantity)) %>%
ggplot(aes(x=n_items))+
geom_histogram(fill="indianred", bins = 100000) +
geom_rug()+
coord_cartesian(xlim=c(0,80))
People mostly purchased less than 10 items (less than 10 items in each invoice).
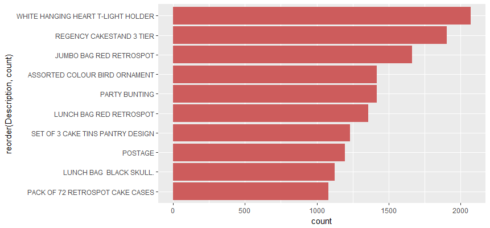
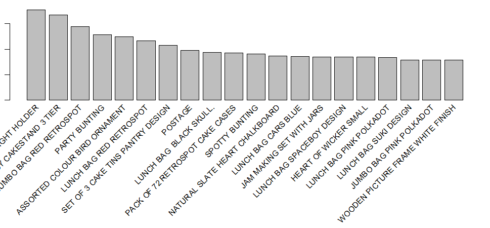
Top 10 best sellers
tmp %>%
group_by(StockCode, Description) %>%
summarize(count = n()) %>%
arrange(desc(count))
tmp %>%
ggplot(aes(x=reorder(Description,count), y=count))+
geom_bar(stat="identity",fill="indian red")+
coord_flip()
# A tibble: 10 x 3
# Groups: StockCode [10]
StockCode Description count
1 85123A WHITE HANGING HEART T-LIGHT HOLDER 2070
2 22423 REGENCY CAKESTAND 3 TIER 1905
3 85099B JUMBO BAG RED RETROSPOT 1662
4 84879 ASSORTED COLOUR BIRD ORNAMENT 1418
5 47566 PARTY BUNTING 1416
6 20725 LUNCH BAG RED RETROSPOT 1358
7 22720 SET OF 3 CAKE TINS PANTRY DESIGN 1232
8 POST POSTAGE 1196
9 20727 LUNCH BAG BLACK SKULL. 1126
10 21212 PACK OF 72 RETROSPOT CAKE CASES 1080
Association rules for online retailer
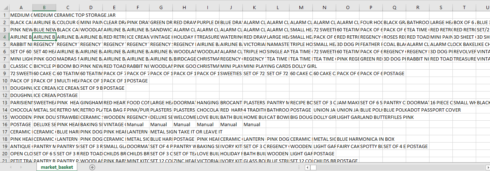
Before using any rule mining algorithm, we need to transform the data from the data frame format, into transactions such that we have all the items bought together in one row. For example, this is the format we need:
retail_sorted <- retail[order(retail$CustomerID),]
library(plyr)
itemList <- ddply(retail,c("CustomerID","Date"),
function(df1)paste(df1$Description,
collapse = ","))
The function ddply() accepts a data frame, splits it into pieces based on one or more factors, computes on the pieces, and then returns the results as a data frame. We use “,” to separate different items.
We only need item transactions, so remove customerID and Date columns.
itemList$CustomerID <- NULL
itemList$Date <- NULL
colnames(itemList) <- c("items")
Write the data fram to a csv file and check whether our transaction format is correct.
write.csv(itemList,"market_basket.csv", quote = FALSE, row.names = TRUE)
Perfect! Now we have our transaction dataset, and it shows the matrix of items being bought together. We don’t actually see how often they are bought together, and we don’t see rules either. But we are going to find out.
Let’s have a closer look at how many transactions we have and what they are.
tr <- read.transactions('market_basket.csv', format = 'basket', sep=',')
tr
summary(tr)
transactions in sparse format with
19296 transactions (rows) and
7881 items (columns)
transactions as itemMatrix in sparse format with
19296 rows (elements/itemsets/transactions) and
7881 columns (items) and a density of 0.002200461
most frequent items:
WHITE HANGING HEART T-LIGHT HOLDER REGENCY CAKESTAND 3 TIER
1772 1667
JUMBO BAG RED RETROSPOT PARTY BUNTING
1445 1279
ASSORTED COLOUR BIRD ORNAMENT (Other)
1239 327226
element (itemset/transaction) length distribution:
sizes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2247 1177 848 762 724 660 614 595 584 553 574 507 490 507 503 504
17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
452 415 474 420 383 309 311 271 236 253 223 204 226 218 174 146
33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
139 145 130 112 116 88 104 94 91 86 94 60 68 74 68 65
49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
52 50 60 51 41 53 51 36 23 40 37 30 31 23 22 24
65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
17 27 32 22 17 25 17 20 18 12 13 19 14 7 9 18
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96
17 11 10 8 12 10 15 7 7 9 6 7 8 5 4 5
97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112
5 3 3 3 5 5 5 2 3 3 8 5 6 3 3 1
113 114 115 116 117 118 119 120 121 122 123 125 126 127 131 132
2 2 1 4 6 3 1 2 1 3 3 4 2 1 1 1
133 134 139 140 141 142 143 145 146 147 149 150 154 157 161 166
4 1 1 1 1 2 1 1 2 1 2 2 2 2 1 1
168 171 177 178 180 194 198 199 202 204 205 209 229 236 249 250
1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1
286 321 401 420
1 1 1 1
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 4.00 12.00 17.34 23.00 420.00
includes extended item information - examples:
labels
1 1 HANGER
2 10 COLOUR SPACEBOY PEN
3 12 COLOURED PARTY BALLOONS
We see 19,296 transactions, and this is the number of rows as well. There are 7,881 items — remember items are the product descriptions in our original dataset. Transactions here are the collections or subsets of these 7,881 items.
The summary gives us some useful information:
-
* density: The percentage of non-empty cells in the sparse matrix. In another word, the total number of items that are purchased divided by the total number of possible items in that matrix. We can calculate how many items were purchased using density like so: 19296 X 7881 X 0.0022.
* The most frequent items should be the same as our results in Figure 3.
* Looking at the size of the transactions: 2247 transactions were for just 1 item, 1177 transactions for 2 items, all the way up to the biggest transaction: 1 transaction for 420 items. This indicates that most customers buy a small number of items in each transaction.
* The distribution of the data is right skewed.
Let’s have a look at the item frequency plot, which should be in aligned with Figure 3.
itemFrequencyPlot(tr, topN=20, type='absolute')
Create some rules
-
* We use the Apriori algorithm in Arules library to mine frequent itemsets and association rules. The algorithm employs level-wise search for frequent itemsets.
* We pass supp=0.001 and conf=0.8 to return all the rules that have a support of at least 0.1% and confidence of at least 80%.
* We sort the rules by decreasing confidence.
Have a look at the summary of the rules:
rules <- apriori(tr, parameter = list(supp=0.001, conf=0.8))
rules <- sort(rules, by='confidence', decreasing = TRUE)
summary(rules)
set of 89697 rules
rule length distribution (lhs + rhs):sizes
2 3 4 5 6 7 8 9 10
103 3206 9909 26451 31144 14599 3464 700 121
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.000 5.000 6.000 5.641 6.000 10.000
summary of quality measures:
support confidence lift count
Min. :0.001036 Min. :0.8000 Min. : 8.711 Min. : 20.00
1st Qu.:0.001088 1st Qu.:0.8333 1st Qu.: 19.052 1st Qu.: 21.00
Median :0.001192 Median :0.8750 Median : 24.495 Median : 23.00
Mean :0.001382 Mean :0.8827 Mean : 49.558 Mean : 26.67
3rd Qu.:0.001503 3rd Qu.:0.9231 3rd Qu.: 42.265 3rd Qu.: 29.00
Max. :0.018242 Max. :1.0000 Max. :622.452 Max. :352.00
mining info:
data ntransactions support confidence
tr 19296 0.001 0.8
The summary of the rules gives us some very interesting information:
-
* The number of rules: 89,697.
* The distribution of rules by length: a length of 6 items has the most rules.
* The summary of quality measures: ranges of support, confidence, and lift.
* The information on data mining: total data mined, and the minimum parameters we set earlier.
We have 89,697 rules. I don’t want to print them all, so let’s inspect the top 10.
inspect(rules[1:10])
lhs rhs support confidence
[1] {WOBBLY CHICKEN} => {DECORATION} 0.001451078 1
[2] {WOBBLY CHICKEN} => {METAL} 0.001451078 1
[3] {DECOUPAGE} => {GREETING CARD} 0.001191957 1
[4] {BILLBOARD FONTS DESIGN} => {WRAP} 0.001502902 1
[5] {WOBBLY RABBIT} => {DECORATION} 0.001762023 1
[6] {WOBBLY RABBIT} => {METAL} 0.001762023 1
[7] {BLACK TEA} => {SUGAR JARS} 0.002332090 1
[8] {BLACK TEA} => {COFFEE} 0.002332090 1
[9] {CHOCOLATE SPOTS} => {SWISS ROLL TOWEL} 0.002176617 1
[10] {ART LIGHTS} => {FUNK MONKEY} 0.002021144 1
lift count
[1] 385.92000 28
[2] 385.92000 28
[3] 344.57143 23
[4] 622.45161 29
[5] 385.92000 34
[6] 385.92000 34
[7] 212.04396 45
[8] 61.06329 45
[9] 410.55319 42
[10] 494.76923 39
The interpretation is pretty straightforward:
-
* 100% customers who bought “WOBBLY CHICKEN” also bought “DECORATION”.
* 100% customers who bought “BLACK TEA” also bought “SUGAR JAR”.
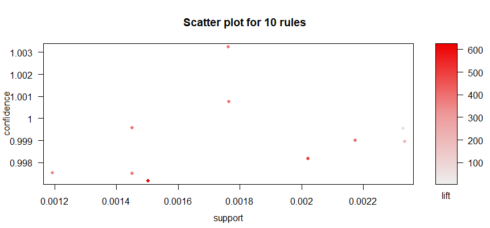
And plot these top 10 rules.
topRules <- rules[1:10] plot(topRules)
plot(topRules, method="graph")
plot(topRules, method = "grouped")
Summary
In this post, we have learned how to perform Market Basket Analysis in R and how to interpret the results. If you want to implement them in Python, Mlxtend is a Python library that has an implementation of the Apriori algorithm for this sort of application. You can find an introduction tutorial here.
If you would like the R Markdown file used to make this blog post, you can find here.
Reference
- R and Data Mining