Panel data, along with cross-sectional and time series data, are the main data types that we encounter when working with regression analysis.
Types of data
- Cross-Sectional: Data collected at one particular point in time
- Time Series: Data collected across several time periods
- Panel Data: A mixture of both cross-sectional and time series data, i.e. collected at a particular point in time and across several time periods
When it comes to panel data, standard regression analysis often falls short in isolating fixed and random effects.
- Fixed Effects: Effects that are independent of random disturbances, e.g. observations independent of time.
- Random Effects: Effects that include random disturbances.
Let us see how we can use the plm library in R to account for fixed and random effects. There is a video tutorial link at the end of the post.
Panel Data: Fixed and Random Effects
For this tutorial, we are going to use a dataset of weekly internet usage in MB across 33 weeks across three different companies (A, B, and C). Find the dataset here: <a href="https://github.com/MGCodesandStats/datasets/blob/master/internetplm.csv.
Let us run our fixed (within) and random (random) effect models:
#Fixed Effects (within) and Random Effects (random)
library(plm)
plmwithin <- plm(usage~income+videohours+webpages+gender+age, data = mydata, model = "within")
plmrandom <- plm(usage~income+videohours+webpages+gender+age, data = mydata, model = "random")
summary(plmwithin)
Oneway (individual) effect Within Model
Call:
plm(formula = usage ~ income + videohours + webpages + gender +
age, data = mydata, model = "within")
Balanced Panel: n=33, T=3, N=99
Residuals :
Min. 1st Qu. Median 3rd Qu. Max.
-7001.684 -1744.973 -18.793 1212.604 6423.064
Coefficients :
Estimate Std. Error t-value Pr(>|t|)
income 0.60389 0.14897 4.0538 0.0001451 ***
videohours 1261.43899 111.13253 11.3508 < 2.2e-16 ***
webpages 97.79839 42.06834 2.3248 0.0234299 *
gender -1328.98316 812.05060 -1.6366 0.1068685
age 54.15710 36.54555 1.4819 0.1435128
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Total Sum of Squares: 4312700000
Residual Sum of Squares: 692730000
R-Squared: 0.83937
Adj. R-Squared: 0.51719
F-statistic: 63.7531 on 5 and 61 DF, p-value: < 2.22e-16
summary(plmrandom)
Oneway (individual) effect Random Effect Model
(Swamy-Arora's transformation)
Call:
plm(formula = usage ~ income + videohours + webpages + gender +
age, data = mydata, model = "random")
Balanced Panel: n=33, T=3, N=99
Effects:
var std.dev share
idiosyncratic 11356210 3370 0.912
individual 1093188 1046 0.088
theta: 0.1191
Residuals :
Min. 1st Qu. Median 3rd Qu. Max.
-8153.757 -1808.112 -90.183 2101.833 8507.735
Coefficients :
Estimate Std. Error t-value Pr(>|t|)
(Intercept) -1831.20613 1482.37880 -1.2353 0.21982
income 0.51416 0.12419 4.1401 7.627e-05 ***
videohours 1265.14090 94.06589 13.4495 < 2.2e-16 ***
webpages 95.35198 37.72137 2.5278 0.01316 *
gender -1688.46458 708.69203 -2.3825 0.01923 *
age 57.27720 30.01488 1.9083 0.05944 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Total Sum of Squares: 5790300000
Residual Sum of Squares: 1031900000
R-Squared: 0.82178
Adj. R-Squared: 0.77198
F-statistic: 85.7674 on 5 and 93 DF, p-value: < 2.22e-16
In the case of the first regression, we are accounting for fixed effects (or internet usage independent of time), while the second is accounting for random effects (including time).
Note that the variables gender and age which were deemed insigificant in the fixed effects regression are now being deemed significant in the random effects regression.
Analysing with fixef
Now, let us use fixef to isolate the effects of time on internet usage.
#Effect of time on internet usage
fixef(plmwithin,type="dmean")
1 2 3 4 5 6 7 8 9 10 11
3054.6050 -467.6298 -1557.9555 524.9491 -18.3859 -1374.6854 2300.6432 1890.2534 -541.1499 4721.5132 241.6241
12 13 14 15 16 17 18 19 20 21 22
-1438.6650 2208.1437 -2036.5721 -848.0145 508.1098 -269.4162 2335.4139 803.8547 -3633.5643 -1399.4824 2142.2455
23 24 25 26 27 28 29 30 31 32 33
258.5465 -2458.9901 -1724.9200 -3979.0983 70.2551 717.6419 1289.9506 -1763.4756 2241.4846 2945.1578 -4742.3872
summary(fixef(plmwithin, type = "dmean"))
Estimate Std. Error t-value Pr(>|t|)
1 3054.605 2860.669 1.0678 0.28561
2 -467.630 2452.521 -0.1907 0.84878
3 -1557.955 2368.244 -0.6579 0.51063
4 524.949 2734.229 0.1920 0.84775
5 -18.386 2861.050 -0.0064 0.99487
6 -1374.685 2719.298 -0.5055 0.61319
7 2300.643 2353.954 0.9774 0.32839
8 1890.253 2598.290 0.7275 0.46692
9 -541.150 2518.805 -0.2148 0.82989
10 4721.513 2619.317 1.8026 0.07146 .
11 241.624 2765.534 0.0874 0.93038
12 -1438.665 2868.905 -0.5015 0.61604
13 2208.144 2651.892 0.8327 0.40503
14 -2036.572 2549.967 -0.7987 0.42448
15 -848.015 2643.324 -0.3208 0.74835
16 508.110 2594.214 0.1959 0.84472
17 -269.416 2463.474 -0.1094 0.91291
18 2335.414 2662.246 0.8772 0.38036
19 803.855 2475.448 0.3247 0.74538
20 -3633.564 2504.424 -1.4509 0.14682
21 -1399.482 2727.735 -0.5131 0.60791
22 2142.245 2477.582 0.8647 0.38723
23 258.546 2702.259 0.0957 0.92378
24 -2458.990 3036.375 -0.8098 0.41803
25 -1724.920 2489.795 -0.6928 0.48844
26 -3979.098 2758.028 -1.4427 0.14910
27 70.255 2595.908 0.0271 0.97841
28 717.642 2494.345 0.2877 0.77357
29 1289.951 2575.964 0.5008 0.61654
30 -1763.476 2458.731 -0.7172 0.47323
31 2241.485 2441.171 0.9182 0.35851
32 2945.158 2725.083 1.0808 0.27980
33 -4742.387 2820.176 -1.6816 0.09265 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Observe that weeks 10 and 33 are significant at the 10% level. For week 10, we see that usage across A, B, and C is higher than usual:

On the other hand, usage for week 33 across A, B, and C is lower than usual:

This could indicate that something is taking place across these particular weeks to cause internet usage to be higher and lower than usual. We see that using fixef has allowed us to isolate the effect of time in this regard.
Now, let us extract fixed effects – i.e. effects independent of time.
#Extracting fixed effects with fixef
twoway <- plm(usage~income+videohours+webpages+gender+age+company,data=mydata,model="within",effect="time")
fixef(twoway,effect="time")
a b c
-451.3598 -1202.3393 -3451.6416
We see that of the three internet companies, company C has the largest negative coefficient.
Let’s subset usage for the three companies and see what is going on:
#Usage by provider a <- subset(mydata, company=="a") b <- subset(mydata, company=="b") c <- subset(mydata, company=="c") #Mean usage by provider mean(a$usage) mean(b$usage) mean(c$usage) [1] 11646.94 [1] 8851.848 [1] 6279.03
We see that mean internet usage for company C is lower than that of A and B.
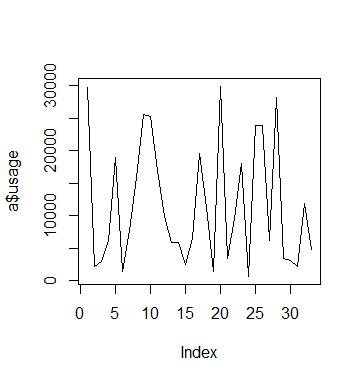
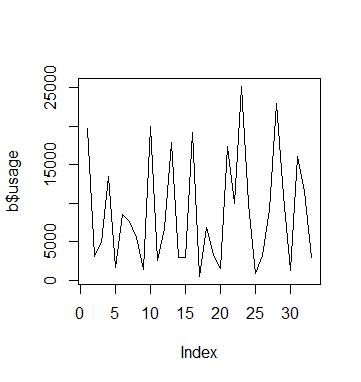
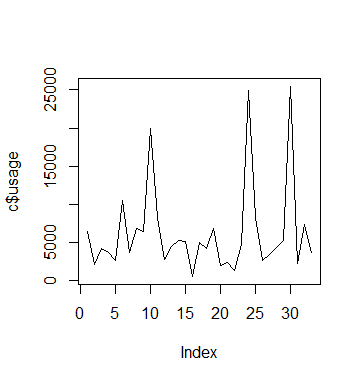
Moreover, visualising usage across the 33 weeks reveals an interesting insight:
#Usage visualisations plot(a$usage,type='l') plot(b$usage,type='l') plot(c$usage,type='l')
We see that in the case of C, usage remains low overall but there are certain periods where we see a spike in usage. However, we see these spikes much more frequently for A and B.
In this regard, comparing fixed and random effects has allowed us to isolate the impact of time on usage patterns for C.
Conclusion
In this tutorial, you have learned:
- The difference between a fixed and random effects model
- How to use the plm library
- How to isolate fixed and random effects in a panel dataset
Many thanks for viewing this tutorial.